제목에 낚였네 ㅎ
본문에서 해석한 것 처럼 <대략 수학적> 이나, <수학스러운> 정도면 좋았을 것 같은데...
낚시 제목을 너무 잘 짓는다!
오히려 책의 내용은 '수학머리' 같은 건 없다는 건데 말이지.
Struggle

1장 수학과 새로운 관계 맺기 ㆍ9
다른 방식 / 좁은 의미의 수학 / 전반적인 문화 문제 / 마인드셋과 인지의 연결 고리 / 성공을 위한 새로운 학습 모델
이 세 가지 악당, 즉 수학 뇌가 존재한다는 생각, 수학 시험을 너무 자주 실시하는 관행, 수학을 절차의 집합으로 생각하는 통념은 현재의 제도적 불평등과 완벽하게 결합해 상당수의 학생에게 끔찍한 경험을 제공하고 있다.
캠프가 끝날 무렵 학생들의 성취도를 테스트한 결과, 4주 동안 우리와 함께한 학생들은 2.8년 동안 학교에서 수학을 공부했을 때 보이는 것과 비슷한 성취도를 보였다. 캠프가 진행되는 동안 학생들은 수학에 대한 마인드셋을 바꿔 자신이 가진 잠재력을 믿기 시작했고, 수학을 다르게 보기 시작했다. 이들의 수학 성취도 향상에 강력한 영향을 미친 것은 수학에 대한 마인드셋과 접근 방식이 같이 바뀌면서 일어난 변화였다.
2장 배우는 법 배우기 ㆍ39
메타인지, 새로운 인지 이론 / 메타인지의 실제 적용 / 메타인지를 촉진하는 8가지 수학 학습 전략 / 저널 쓰기 / 성찰과 성장 마인드셋 구축하기 / 그룹 활동을 통해 메타인지를 촉진하는 법: 서로의 생각을 존중하도록 가르치기 / 메타인지를 장려하는 평가란 무엇인가
전략
1. 한 걸음 물러서기
2. 문제를 그림으로 그리기
3. 새로운 접근 방식 찾기
4. "왜?"에 대해 생각해보기
5. 단순화하기
6. 추측하기
7. 회의론자 되기
8. 더 작은 사례 시도하기
3장 성장 마인드셋 장착하기 ㆍ85
우리는 왜 애씀을 사랑해야 하는가 / 아이들이 애씀의 버스에 오르게 하려면
학교뿐만 아니라 사회에서도 실수와 애씀에 대해 두려움을 갖는 문화를 바꿔야 할 필요가 있다. 실수하는 시간과 애쓰는 시간은 둘 다 뇌가 지식을 늘리고 창의성을 발달시키는 데 매우 중요하면서 가치가 크기 때문이다.
학습자들이 애씀과 실수에 익숙해지도록 도우려면 먼저 우리가 그것들에 익숙해져야 한다. 그러려면 우리 모두가 때때로 자신에게 하는 부정적인 말을 하지 않도록 노력해야 한다. 우리가 먼저 불확실성, 실수, 애씀에 익숙해지면, 우리 모습이 다른 어른들과 학습자들에게 그러한 것들을 경험하는 시기에 편안해질 수 있음을 보여주는 모범적인 예가 될 수 있다. 여러분이 이 여정의 어느 단계에 있든, 이 장이 학습자를 위해 실수 친화적인 환경을 조성하고 도전과 실수의 시간을 받아들이는 데 도움이 되는 아이디어와 자원의 공유에 일조하기를 바란다. 학습은 결과가 아니라 과정이며, 애를 쓸 때야말로 가장 역동적인 기회가 생겨난다.
4장 세상 속 진짜 수학 ㆍ123
중요한 것을 배우고 가르치기 / 핵심 영역 1: 수 감각 / 핵심 영역 2: 데이터 리터러시 / 핵심영역 3: 선형방정식 / 수학의 쓸모: 데이터 인식
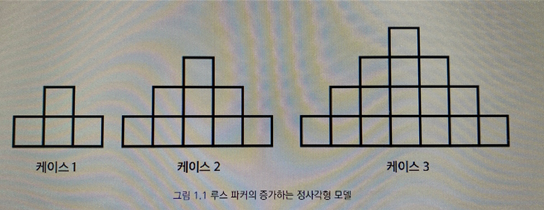
수는 항상 시각적으로 볼 수 있으며, 시각적 요소는 더 깊은 의미를 더한다. 초등학교 교사들과 함께 일할 때 그중 한 명이 제곱수는 정사각형square 으로 표현할 수 있기 때문에 정사각수square number 라고도 부른다는 사실을 예전엔 몰랐었다며 기뻐하던 기억이 난다.
•누가 이 데이터를 생산했는가? 이 데이터를 생산한 목적은 무엇인가?
•모든 데이터가 표시되고 있는가? 그렇지 않다면 무엇이 생략되어 있는가?
•그래프의 축과 범례의 내용이 합리적인가? 아니면, 요점을 강조하기 위해 만들어진 것인가?
•어떤 관계가 분명하게 드러나는가?
•관계가 인과관계인가, 아니면 단순한 상관관계인가?
5장 시각적 경험으로서의 수학 ㆍ175
정신적 표현 / 정신적 표현의 신경과학 / 그룹화 / 수학적으로 다양한 연산
...3/4은 한 번에 1에 전체가 들어가고 일부 빈 곳을 남긴다는 것을 알 수 있다. 3/4이 다시 이 빈 곳에 들어가려면, 그 3/4의 1/3만 들어갈 수 있다. 이렇게 생각하면 1과 1/3이라는 답이 나온다. 3/4은 1이라는 전체 공간 안에 한 번 들어가고, 나머지 공간에는 그 3/4의 1/3이 한 번 들어갈 수 있다는 뜻이다. 분수 나누기 과정을 시각적으로, 그리고 대략이라는 렌즈를 통해 보는 일은 뒤집고 곱하는 일보다 시간이 조금 더 걸릴 수 있지만, 그 이후로 계산과 규칙을 사용하는 모든 작업을 할 때 떠올릴 수 있는 정신적 표현을 제공한다. (1 나누기 3/4)
6장 수학적 개념을 연결하기 ㆍ225
핵심은 수 감각 / 표준의 문제 / 수학적 연결 / 개념과 연결성을 가르치자 / 개념적 교육과 연계된 성공
하나의 크고 아름다운 아이디어가 이 과목을 처음부터 끝까지 관통한다. 이 아이디어를 인식하게 되면, 미적분의 구조는 통일된 주제에 대한 변형으로 제자리를 잡게 된다. 안타깝게도, 대부분의 미적분학 강의는 공식, 절차, 계산 기법이라는 눈사태 속에 이 주제를 묻어버린다. 실제로 이 주제는 미적분학 문화의 일부이고 모든 전문가가 암묵적으로 알고 있는 것임에도, 어디에서도 이에 대해 설명하는 것을 본 적이 없다. 이것을 무한대 원리 Infinity Principle 라고 부르자. 이 원리가 우리의 여정을 안내할 것이다.
...
미적분은 절단과 재구성의 두 단계로 진행된다. 수학적으로 잘라내는 과정에는 항상 무한히 미세한 뺄셈이 포함되며, 이는 부분 사이의 차이를 정량화하는 데 사용된다. 따라서 이 절반의 과정을 미분이라고 부른다. 재구성 과정에는 항상 무한한 덧셈이 포함되며, 이는 각 부분을 원래의 전체로 다시 통합한다. 이 절반의 과정을 적분이라고 부른다. <미적분의 힘 Infinite Power>
7장 연습과 피드백의 재설계 ㆍ267
다양하고 신중한 연습이란 무엇인가 / 다양한 방식의 연습 사례 / 더 많이 보기 / 절차적 문제와 개념적 문제 / 수학 예제에 다양성 적용하기 / 피드백 고리를 통한 평가 / 피드백 고리를 이용해 가르치기
8장 새로운 수학 공부의 미래 ㆍ303
형평성과 전문성을 위한 새로운 모델 / 데이터 조사를 통한 다양한 참여 / 교사 한 명의 영향력 / 수학의 현 상태 뒤집기 / 조직적인 인종차별과 편견 / 효과적인 변화를 위한 5가지 원칙
'책 이야기' 카테고리의 다른 글
| 아무도 상처받지 않는 대화법: 칭찬보다 더 효과적인 말투의 심리학 (0) | 2024.12.30 |
|---|---|
| 내 방식대로 삽니다 (1) | 2024.12.27 |
| 하버드 새벽4시반: 세계 최고의 대학, 하버드가 들려주는 성공 습관 (0) | 2024.12.18 |
| 50 오늘이 당신에게 가장 젊은 날입니다: 인생후반전, 후회 없는 삶을 위한 힌트 (50代がもっともっと樂しくなる方法) (2) | 2024.12.17 |
| 엘리트 세습 (The Meritocracy Trap) (5) | 2024.12.12 |




댓글